When Chad Holbrook took over as head coach we knew not everything would be the same as it was under Ray Tanner. Something that has seemed different this year is the frequency with which our runners attempt to steal bases and the frequency with which they get caught. One of those is true; the other just seems that way.
South Carolina is stealing with more frequency, but they aren't getting caught as often. South Carolina has stolen 23 bases in 33 attempts thus far this season. (All Stats through the Missouri series.) That is 1.65 attempts per game and a 69.70% success rate. Last year Carolina took off 1.03 times per game and succeeded 61.97% of the time. In 2011 USC attempted 0.86/game and succeeded 69.49% of those attempts. In 2010 it was 1.07/game and 70.67%.
2013's success rate is in-line with historical norms and an improvement from last season. Still, they aren't being successful enough. Whether to steal or not is a matter of playing the odds, and right now, we aren't doing that.
Baseball lends itself well to statistical analysis and in any given situation there are expected outcomes. Most of us assume that when the bases are loaded with no outs the batting team is likely to score more runs that inning than an inning when there are no runners on and two outs. Statistical analysis would confirm this assumption. In fact, it is the acknowledgement of this proposition that makes stealing bases attractive. All other things being equal, a runner on second is better than a runner on first. The big question is: how much better? And how much worse is it to have no runners and an out?
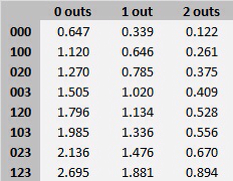
There is an excellent site out there Tango Tiger that will allow you to input data and get the expected runs matrix out of it. I've input the data for South Carolina from the beginning of 2010 to present. Here is the expected runs matrix:
Since we know the values we can evaluate South Carolina's strategy. The chart tells us that when there is a runner on first base an nobody out, the expected runs for that inning are 1.120. If that runner successfully steals second the expected runs would increase to 1.270. If the runner is thrown out, then there will be no runners and one out which yields an expected run value of 0.339 runs.
If South Carolina could steal a base safely everytime, have 100% success, they should obviously do it every time. If it was 99% they should probably run all the time too. But at some point the strategy yields fewer runs. At what point? If we look at the chart, it is a matter of algebra.
Take our earlier example of a runner on first with no outs. Here is the formula for determining what percentage of the time we need to successfully steal in order to steal in that situation:
1.120 = 1.270x + 0.339(1-x)
1.120 is our current situation (runner on first, no outs). 1.270 is if the runner is safe (runner on second, no outs). 0.339 is an out and no runners. x is our success rate. If you do the math you get 0.8389 or 83.89%. If you can successfully steal more than 83.89 % of the time you can expect to score more runs by trying to steal second in this situation. If you cannot steal with that much success you are taking runs off the board. Currently we are succeeding just under 70% of the time.
That doesn't mean we shouldn't steal ever. There may be times when we should steal. Here are some scenarios and the success rate needed. I only ran these for stealing one base at a time since we don't double steal very often at all. I also didn't worry about stealing home given its rarity.
- Runner on 1st, no outs: 83.89 %
- Runner on 1st, one out: 79.03 %
- Runner on 1st, two outs: 69.46 %
- Runner on 2nd, no outs: 79.85 %
- Runner on 2nd, one out: 73.83%
- Runner on 2nd, two outs: 91.69 %
- Runners on 1st and 3rd, no outs: 86.47%
- Runners on 1st and 3rd, one out: 86.88%
- Runners on 1st and 3rd, two outs: 82.99%
With these situations and our success rate, we should really only be stealing with a runner on 1st and two outs or perhaps a runner on 2nd and one out. Why? With a runner on first and two outs, it is probably going to take two hits or something similar to get a run home. Stealing second cuts the need in half: you can probably score with just one hit, which is much more likely to occur. If you are thrown out you really don't give up that much since you weren't likely to score from first anyway.
With a runner on second and one out, you need a hit, probably. If you steal third, a sacrifice fly or deep ground ball should score the runner. You don't really need another hit, so there is a great deal to be gained.
South Carolina is definitely stealing more, and we probably shouldn't be. We need to be a little more successful to justify all the risk we're taking. It's an early season, so we'll see. Check back later; we'll re-run the numbers and see if we are right.